sábado, junho 10, 2006
Distância média percorrida num armazém com duas portas do mesmo lado
Suponha-se que a região de armazenagem se localiza no primeiro e quarto quadrantes, duas portas (P1 e P2) se localizam ao longo do eixo dos y's separadas pela distância c, a movimentação rectilinear de/para o armazém tem igual probabilidade de ocorrência para cada porta e é necessária uma área de armazenagem A.
Na Figura 1, r é a distância rectilinear desde a intersecção da linha de isocusto com o eixo dos y's à porta mais próxima. A linha de isocusto envolve uma área de
A = r (c + r)
A linha de contorno é um trapézio cuja área é dada por
A = h × (a + b) / 2
onde a é o comprimento da base menor, b o comprimento da base maior e h a altura do trapézio. Assim, a área limitada pela linha de isocusto da Figura 1 pode ser expressa como
r × (c + 2 × r + c) / 2 = r (c + r)
Resolvendo em ordem a r tem-se
0,5 [(4 A + c2)½ - c]
Se um peso de 0,5 for associado a cada porta, a relação entre r e k, o valor da linha de isocusto, é dada por
Na Figura 1, r é a distância rectilinear desde a intersecção da linha de isocusto com o eixo dos y's à porta mais próxima. A linha de isocusto envolve uma área de
A = r (c + r)
A linha de contorno é um trapézio cuja área é dada por
A = h × (a + b) / 2
onde a é o comprimento da base menor, b o comprimento da base maior e h a altura do trapézio. Assim, a área limitada pela linha de isocusto da Figura 1 pode ser expressa como
r × (c + 2 × r + c) / 2 = r (c + r)
Resolvendo em ordem a r tem-se
0,5 [(4 A + c2)½ - c]
Se um peso de 0,5 for associado a cada porta, a relação entre r e k, o valor da linha de isocusto, é dada por
k = 0,5 r + 0,5 (r + c )
ou
r = k - 0,5 c
Figura 1. Região de armazenagem contínua com duas portasSubstituindo r, na primeira equação, pelo valor de r dado pela última equação, obtém-se
A = (k - 0,5 c) × (k + 0,5 c)
ou
A = k2 - 0,25 c2 = q (k)
Para além disso, resolvendo para k como uma função de A,
k = (A + 0,25 c2)½ = r (A)
e
r (0) = 0,5 c
A = (k - 0,5 c) × (k + 0,5 c)
ou
A = k2 - 0,25 c2 = q (k)
Para além disso, resolvendo para k como uma função de A,
k = (A + 0,25 c2)½ = r (A)
e
r (0) = 0,5 c
A distância média percorrida é dada por
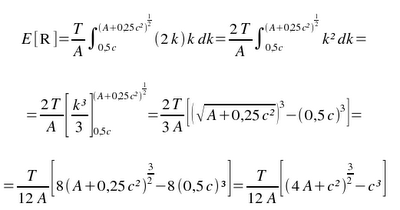
Suponha-se que a área de armazenagem delimitada pela linha de isocusto tem 10 000 ft2, que as portas estão separadas por uma distância de 20 ft e são feitas 100 operações de entrada / saída por hora. Para c = 20 ft, T = 100 por hora e A = 10 000 ft2, E [R] = 6 760,25 ft/hora.
FRANCIS, Richard L.; et al. - Facility Layout and Location: An Analytical Approach, 2.ª ed., Englewood Cliffs, NJ, Prentice Hall, 1992.
