sábado, junho 10, 2006
Seminário Moodle@FCTUNL
Quarta-feira, 28 de Junho de 2006
Local e Hora: Ed. VII, sala 1.14, das 14:30 às 17:30
- Objectivos
- Apresentar e discutir alguns exemplos relevantes do uso da tecnologia na educação pelos professores e alunos da FCTUNL.
- Reflectir sobre o papel das tecnologias no ensino e na aprendizagem e o seu potencial na FCTUNL.
- Programa
- Cada apresentação demorará cerca de 10 min, seguida de 10 min de discussão.
15:35-16:00 – Alunos de Logística (Licenciatura em Engenharia e Gestão Industrial)
Blogs e aprendizagem
Distância média percorrida por dois produtos num armazém com duas portas do mesmo lado
Considere-se o exemplo anterior, mas com várias classes de produtos. Então para o produto j:
q (kj) = kj2 - 0,25 c2
r (Bj) = (Bj + 0,25 c2)½
onde Bj = A1 + ... + Aj. Para o caso de três classes de produtos, a distância média percorrida é dada por:
q (kj) = kj2 - 0,25 c2
r (Bj) = (Bj + 0,25 c2)½
onde Bj = A1 + ... + Aj. Para o caso de três classes de produtos, a distância média percorrida é dada por:
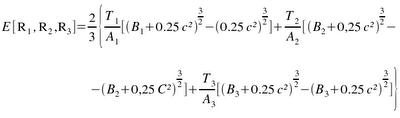
Suponha-se são feitas 100 movimentações por hora e que o espaço total necessário são 10 000 ft2. Os produtos da Classe I representam 75% das movimentações e 15% das necessidades de espaço; os produtos da Classe II representam 20% das movimentações e 35% do espaço de armazenagem; e os produtos da classe II representam 5% das movimentações e 50% do espaço. Fazendo T1 = 75, A1 = 1 500, T2 = 20, A2 = 3 500, T3 = 5 e A3 = 5 000, as razões entre as movimentações e os espaços para as três classes de produtos são 0,05, 0,0057 e 0,001. Com c = 20 ft, a distância média percorrida para as três classes é de 3 677,49 ft/hora.
Para estabelecer um limite superior para o espaço necessário em armazenagem aleatória resultar na mesma distância média percorrida em armazenagem dedicada das três classes de produtos, faz-se a distância média percorrida por uma classe de produtos de área desconhecida igual à distância média percorrida pelas três classes de produtos. Então, da última equação da entrada anterior, com c = 20 ft, T = 100 por hora e E [R] = 3 677,49 ft/hr,
100 [(4 Ars + 202)½ - 203] / (12 Ars) = 3 677,49
Resolvendo em ordem a Ars por métodos numéricos resulta um valor aproximado de 2 771,86 ft2. Portanto, com base nos resultados obtidos, para um armazém com duas portas do mesmo lado e três classes de produtos com as razões entre as movimentações e o espaço dadas, em comparação com os 10 000 ft2 para a armazenagem dedicada, o espaço necessário para a armazenagem aleatória não pode exceder 27,72% da área do sistema de armazenagem dedicada para se obter o mesmo valor para a distância média percorrida.
Para estabelecer um limite superior para o espaço necessário em armazenagem aleatória resultar na mesma distância média percorrida em armazenagem dedicada das três classes de produtos, faz-se a distância média percorrida por uma classe de produtos de área desconhecida igual à distância média percorrida pelas três classes de produtos. Então, da última equação da entrada anterior, com c = 20 ft, T = 100 por hora e E [R] = 3 677,49 ft/hr,
100 [(4 Ars + 202)½ - 203] / (12 Ars) = 3 677,49
Resolvendo em ordem a Ars por métodos numéricos resulta um valor aproximado de 2 771,86 ft2. Portanto, com base nos resultados obtidos, para um armazém com duas portas do mesmo lado e três classes de produtos com as razões entre as movimentações e o espaço dadas, em comparação com os 10 000 ft2 para a armazenagem dedicada, o espaço necessário para a armazenagem aleatória não pode exceder 27,72% da área do sistema de armazenagem dedicada para se obter o mesmo valor para a distância média percorrida.
FRANCIS, Richard L.; et al. - Facility Layout and Location: An Analytical Approach, 2.ª ed., Englewood Cliffs, NJ, Prentice Hall, 1992.
Distância média percorrida num armazém com duas portas do mesmo lado
Suponha-se que a região de armazenagem se localiza no primeiro e quarto quadrantes, duas portas (P1 e P2) se localizam ao longo do eixo dos y's separadas pela distância c, a movimentação rectilinear de/para o armazém tem igual probabilidade de ocorrência para cada porta e é necessária uma área de armazenagem A.
Na Figura 1, r é a distância rectilinear desde a intersecção da linha de isocusto com o eixo dos y's à porta mais próxima. A linha de isocusto envolve uma área de
A = r (c + r)
A linha de contorno é um trapézio cuja área é dada por
A = h × (a + b) / 2
onde a é o comprimento da base menor, b o comprimento da base maior e h a altura do trapézio. Assim, a área limitada pela linha de isocusto da Figura 1 pode ser expressa como
r × (c + 2 × r + c) / 2 = r (c + r)
Resolvendo em ordem a r tem-se
0,5 [(4 A + c2)½ - c]
Se um peso de 0,5 for associado a cada porta, a relação entre r e k, o valor da linha de isocusto, é dada por
Na Figura 1, r é a distância rectilinear desde a intersecção da linha de isocusto com o eixo dos y's à porta mais próxima. A linha de isocusto envolve uma área de
A = r (c + r)
A linha de contorno é um trapézio cuja área é dada por
A = h × (a + b) / 2
onde a é o comprimento da base menor, b o comprimento da base maior e h a altura do trapézio. Assim, a área limitada pela linha de isocusto da Figura 1 pode ser expressa como
r × (c + 2 × r + c) / 2 = r (c + r)
Resolvendo em ordem a r tem-se
0,5 [(4 A + c2)½ - c]
Se um peso de 0,5 for associado a cada porta, a relação entre r e k, o valor da linha de isocusto, é dada por
k = 0,5 r + 0,5 (r + c )
ou
r = k - 0,5 c
Substituindo r, na primeira equação, pelo valor de r dado pela última equação, obtém-se
A = (k - 0,5 c) × (k + 0,5 c)
ou
A = k2 - 0,25 c2 = q (k)
Para além disso, resolvendo para k como uma função de A,
k = (A + 0,25 c2)½ = r (A)
e
r (0) = 0,5 c
A = (k - 0,5 c) × (k + 0,5 c)
ou
A = k2 - 0,25 c2 = q (k)
Para além disso, resolvendo para k como uma função de A,
k = (A + 0,25 c2)½ = r (A)
e
r (0) = 0,5 c
A distância média percorrida é dada por
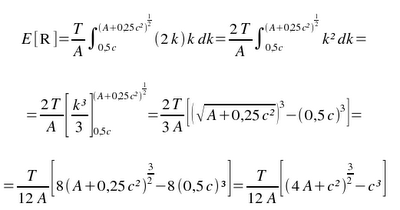
Suponha-se que a área de armazenagem delimitada pela linha de isocusto tem 10 000 ft2, que as portas estão separadas por uma distância de 20 ft e são feitas 100 operações de entrada / saída por hora. Para c = 20 ft, T = 100 por hora e A = 10 000 ft2, E [R] = 6 760,25 ft/hora.
FRANCIS, Richard L.; et al. - Facility Layout and Location: An Analytical Approach, 2.ª ed., Englewood Cliffs, NJ, Prentice Hall, 1992.
Distância média percorrida por dois produtos num armazém com uma porta
Considere-se o exemplo anterior com dois produtos, 1 e 2. As necessidades de espaço são, respectivamente, S1 = 2 500 ft2 e S2 = 2 400 ft2. As movimentações são, respectivamente, T1 = 100 e T2 = 50 por dia. As áreas de armazenagem dos dois produtos num espaço com uma única porta são ilustradas na Figura 1.
Por extensão dos resultados para um único produto, a distância média percorrida é dada por

onde T1 e T2 são os valores das movimentações dos produtos 1 e 2, respectivamente.
Os limites do segundo integral resultam da linha de isocusto que limita a região do produto 2 tomar os valores expressos em termos da área total de armazenagem envolvida. Desta forma, as linhas de contorno para o produto 2 variam em valor desde o máximo para o produto 1 até um valor que coincide com a envolvente das áreas conjuntas dos dois produtos. Assim sendo,
Os limites do segundo integral resultam da linha de isocusto que limita a região do produto 2 tomar os valores expressos em termos da área total de armazenagem envolvida. Desta forma, as linhas de contorno para o produto 2 variam em valor desde o máximo para o produto 1 até um valor que coincide com a envolvente das áreas conjuntas dos dois produtos. Assim sendo,

FRANCIS, Richard L.; et al. - Facility Layout and Location: An Analytical Approach, 2.ª ed., Englewood Cliffs, NJ, Prentice Hall, 1992.
Cálculo da distância média percorrida num armazém
No caso de locais de armazenagem discretos, a distância média percorrida, dentro da zona de armazenagem, pode ser determinada somando as distâncias médias de cada produto. Esta distância pode ser determinada somando as distâncias percorridas de e para todos os locais de armazenagem afectados a um produto, dividindo a soma pelo número de locais afectados ao produto e multiplicando o resultado pelo número médio de movimentações efectuadas por período de tempo, pelo produto. De forma semelhante, no caso de armazenagem contínua, a distância média, para uma região de armazenagem dedicada a um produto, pode ser obtida integrando a região de armazenagem e multiplicando o resultádo pela razão entre o número de movimentações e o espaço afectado ao produto.
Em alternativa à integração sobre toda a região, é possível integrar ao longo das linhas de isocusto que definem a região. Para fazer isso, é necessário desenvolver uma relação funcional entre o valor de uma linha de isocusto e a área que envolve. Para facilitar a descrição da abordagem da «integração pela linha de isocusto», considere-se a Figura 1, envolvendo a utilização de armazenagem aleatória.
Em alternativa à integração sobre toda a região, é possível integrar ao longo das linhas de isocusto que definem a região. Para fazer isso, é necessário desenvolver uma relação funcional entre o valor de uma linha de isocusto e a área que envolve. Para facilitar a descrição da abordagem da «integração pela linha de isocusto», considere-se a Figura 1, envolvendo a utilização de armazenagem aleatória.
A região de armazenagem é servida por um única porta, localizada na origem; a região de armazenagem está contida no primeiro e quarto quadrantes; supõe-se que as movimentações são rectilineares.
Como se mostra na Figura 1, a linha de isocusto resultante é um triângulo. Escolhendo uma linha de isocusto arbitrária qualquer de valor k, a área envolvida (A) é igual a k2. Portanto,
A = k2 = q (k)
q (k) é a relação funcional entre A e k; especificamente, é a área de um conjunto de nívelde valor k. Mais ainda, invertendo a equação anterior,
k = A½ = r (A)
r (A) é a função inversa que relaciona k com A e determina-se resolvendo q (k) em ordem a k. A função inversa de r (t) pode ser calculada a partir de A = q (r (t)). Por exemplo, q (k) = k2 resulta em A = r (A)2 ou r (A) = A½.
Geralmente, à medida que uma linha de isocusto varia do valor mínimo ao máximo, a área envolvida varia do valor mínimo ao valor A. Neste caso, o valor mínimo da linha de isocusto pode ser obtido a partir da equação anterior, fazendo A igual a zero; o valor máximo pode ser obtido igualando a mesma equação à área de armazenagem a envolver.
No exemplo da Figura 1 a área limitada é de 152 000 ft2. Aplicando a equação k = A½ = r (A), o valor mínimo da linha de isocusto é zero e o valor máximo é 389,8717 ft. Para calcular a distância média percorrida, pode-se usar a seguinte expressão com um integral simples:
Como se mostra na Figura 1, a linha de isocusto resultante é um triângulo. Escolhendo uma linha de isocusto arbitrária qualquer de valor k, a área envolvida (A) é igual a k2. Portanto,
A = k2 = q (k)
q (k) é a relação funcional entre A e k; especificamente, é a área de um conjunto de nívelde valor k. Mais ainda, invertendo a equação anterior,
k = A½ = r (A)
r (A) é a função inversa que relaciona k com A e determina-se resolvendo q (k) em ordem a k. A função inversa de r (t) pode ser calculada a partir de A = q (r (t)). Por exemplo, q (k) = k2 resulta em A = r (A)2 ou r (A) = A½.
Geralmente, à medida que uma linha de isocusto varia do valor mínimo ao máximo, a área envolvida varia do valor mínimo ao valor A. Neste caso, o valor mínimo da linha de isocusto pode ser obtido a partir da equação anterior, fazendo A igual a zero; o valor máximo pode ser obtido igualando a mesma equação à área de armazenagem a envolver.
No exemplo da Figura 1 a área limitada é de 152 000 ft2. Aplicando a equação k = A½ = r (A), o valor mínimo da linha de isocusto é zero e o valor máximo é 389,8717 ft. Para calcular a distância média percorrida, pode-se usar a seguinte expressão com um integral simples:

onde E[R] é a distância média percorrida na região de armazenagem R, T é o número de «viagens» de e para o armazém por unidade de tempo (i.e., as movimentações), f (X) é a distância média por viagem de ou para o ponto X, e q' (k) é a primeira derivada de q (k) em ordem a k.
Para explicar a equação anterior, note-se que a função distrubição para a distância percorrida é dada por q (k) / A; portanto a função densidade é dada por q' (k) / A para r (0) ≤ k ≤ r (A). Portanto a distância média percorrida é como indicado acima.
Para ilustrar o uso da equação anterior no cálculo da distância média percorrida, considere o exemplo da Figura 1. Aplicando a equação anterioir temos:
 Portanto, para a movimentação de uma unidade por minuto e uma área de 152 000 ft2, E[R] = 259,9145 ft/min.
Portanto, para a movimentação de uma unidade por minuto e uma área de 152 000 ft2, E[R] = 259,9145 ft/min.
FRANCIS, Richard L.; et al. - Facility Layout and Location: An Analytical Approach, 2.ª ed., Englewood Cliffs, NJ, Prentice Hall, 1992.
Para explicar a equação anterior, note-se que a função distrubição para a distância percorrida é dada por q (k) / A; portanto a função densidade é dada por q' (k) / A para r (0) ≤ k ≤ r (A). Portanto a distância média percorrida é como indicado acima.
Para ilustrar o uso da equação anterior no cálculo da distância média percorrida, considere o exemplo da Figura 1. Aplicando a equação anterioir temos:
 Portanto, para a movimentação de uma unidade por minuto e uma área de 152 000 ft2, E[R] = 259,9145 ft/min.
Portanto, para a movimentação de uma unidade por minuto e uma área de 152 000 ft2, E[R] = 259,9145 ft/min.FRANCIS, Richard L.; et al. - Facility Layout and Location: An Analytical Approach, 2.ª ed., Englewood Cliffs, NJ, Prentice Hall, 1992.
Regiões de armazenagem dedicada para dois produtos
Considerem-se dois produtos, 1 e 2. As necessidades de espaço são, respectivamente, S1 = 2 500 ft2 e S2 = 2 400 ft2. As movimentações são, respectivamente, T1 = 100 e T2 = 50 por dia. T1 / S1 = 0,04 e T2 / S2 = 0,021. Como (T1 / S1) > (T2 / S2) o produto 1 é colocado no layout primeiro. Para delimitar a zona ocupada pelo produto 1 é necessário construir uma linha de isocusto que delimite a área de 2 500 ft2. Existe uma única porta, localizada ao longo do eixo y's e a região de armazenagem deve ocupar apenas o primeiro e quarto quadrantes. Então uma região de armazenagem triangular com 100 ft de base e 50 ft de profundidade ou altura é afectada ao produto 1. A união das duas áreas de armazenagem é também limitada por uma linha de isocusto triangular. Como as duas áreas combinadas somam 4 900 ft2, esta área deve ser limitada por uma linha de isocusto triangular com 140 ft de base e 70 ft de altura, como se mostra na Figura 1.
FRANCIS, Richard L.; et al. - Facility Layout and Location: An Analytical Approach, 2.ª ed., Englewood Cliffs, NJ, Prentice Hall, 1992.
Configuração contínua de armazém
Em várias situações práticas o projecto de layout é para mum armazém já existente. Para ilustrar a abordagem seguida, considere-se um armazém com as dimensões 200 ft × 150 ft com uma única porta localizada como se mostra na Figura 1.
É utilizada armazenagem aleatória e o espaço necessário é de 18 000 ou 27 500 ft2. Supõe-se que a probabilidade da movimentação de um artigo entre a porta e qualquer ponto no espaço de armazenagem é a mesma e supõe-se que as deslocações são rectilineares.
Construindo curvas de nível dentro do armazém existente resulta em três famílias diferentes de formas geométricas, cono se mostra na Figura 2.
Construindo curvas de nível dentro do armazém existente resulta em três famílias diferentes de formas geométricas, cono se mostra na Figura 2.
A linha de isocusto de menor valor tem forma triangular e é aplicável a áreas que não excedam 10 000 ft2; o conjunto seguinte de linhas de isocusto aplica-de a áreas entre 10 000 ft2 e 20 000 ft2; e o último conjunto de linhas de isocusto aplica-se a áreas de armazenagem entre 20 000 ft2 e 30 000 ft2.
A área de armazenagem (A) delimitada por uma linha de isocusto pode ser expressa como uma função do valor da linha de isocusto (k) da seguinte forma:
A área de armazenagem (A) delimitada por uma linha de isocusto pode ser expressa como uma função do valor da linha de isocusto (k) da seguinte forma:

No primeiro caso, a curva de nível tem forma triangular com uma base igual a 2 × k e uma altura de k; a área é k2 com valores de k a variarem de 0 a 100 ft enquanto a área interior varia de 0 a 10 000 ft2.
No segundo caso, começando no ponto onde a linha de isocusto intersecta a parede superior da instalação, a distância da linha de isocusto ao ponto de entrada / saída é a soma de 100 ft percorridos paralelamente ao eixo dos y's e (k - 100) ft percorridos paralelamente ao eixo dos x's. A linha de isocusto varia entre 100 e 150 ft à medida que a ára de armazenagem varia de 10 000 a 20 000 ft2. A forma geométrica da linha de isocusto pode ser representada como a união de um rectângulo de dimensões 200 ft × (k - 100) ft e um triângulo de 200 ft de base e 100 ft de altura. Assim, a área limitada pela linha de isocusto é 200 k - 10 000.
No terceiro caso, a área limitada pela linha de isocusto pode ser obtida simplesmente subtraindo a área exterior à linha de isocusto, da área total do edifício. Cada canto do edifício fora da linha de isocusto tem uma forma triangular de dimensões (250 - k) × (250 - k). Então, a área limitada pela linha de isocusto é igual à área do edifício, 30 000, menos a soma das áreas dos dois cantos, (250 - k)2. As linhas de isocusto variam entre valores de 150 a 250 ft enquanto a área de armazenagem varia de 20 000 a 30 000 ft2.
Fazendo A igual a 18 000 e resolvendo em ordem a k dá um valor de 140 ft (usando a equação A = 200 k - 10 000) e o resultado pode ser observado na Figura 3.
No segundo caso, começando no ponto onde a linha de isocusto intersecta a parede superior da instalação, a distância da linha de isocusto ao ponto de entrada / saída é a soma de 100 ft percorridos paralelamente ao eixo dos y's e (k - 100) ft percorridos paralelamente ao eixo dos x's. A linha de isocusto varia entre 100 e 150 ft à medida que a ára de armazenagem varia de 10 000 a 20 000 ft2. A forma geométrica da linha de isocusto pode ser representada como a união de um rectângulo de dimensões 200 ft × (k - 100) ft e um triângulo de 200 ft de base e 100 ft de altura. Assim, a área limitada pela linha de isocusto é 200 k - 10 000.
No terceiro caso, a área limitada pela linha de isocusto pode ser obtida simplesmente subtraindo a área exterior à linha de isocusto, da área total do edifício. Cada canto do edifício fora da linha de isocusto tem uma forma triangular de dimensões (250 - k) × (250 - k). Então, a área limitada pela linha de isocusto é igual à área do edifício, 30 000, menos a soma das áreas dos dois cantos, (250 - k)2. As linhas de isocusto variam entre valores de 150 a 250 ft enquanto a área de armazenagem varia de 20 000 a 30 000 ft2.
Fazendo A igual a 18 000 e resolvendo em ordem a k dá um valor de 140 ft (usando a equação A = 200 k - 10 000) e o resultado pode ser observado na Figura 3.
Fazendo A igual a 27 500 e resolvendo em ordem a k dá um valor de 200 ft [usando a equação A = 30 000 - (250 - k2)] e resulta na configuração que pode ser observada na Figura 4.
FRANCIS, Richard L.; et al. - Facility Layout and Location: An Analytical Approach, 2.ª ed., Englewood Cliffs, NJ, Prentice Hall, 1992.
Dimensionamento de armazém com base nos custos
Suponha-se que só se tem que armazenar um artigo. Defina-se um horizonte de planeamento T = 10 períodos de tempo. O custo fixo actualizado por unidade de capacidade de armazagem que se possui, durante o horizonte de planeamento, C0, é de 20 UM. O valor presente do custo de posse por unidade armazenada no espaço que se possui por período de tempo, C1, é de 1 UM e num espaço alugado, C2, é de 4 UM. As necessidades de espaço, ao longo do horizonte de planeamento, são: 4, 6, 8, 10, 9, 8, 7, 6, 5, e 4 para os períodos de tempo 1 a 10, respectivamente.
As procuras por período e por ordem decrescente, as respectivas frequências e soma cumulativa parcial das frequências estão representadas na Tabela 1. C' = C0 / (C2 - C1) = 20 / (4 - 1) = 6,7 e a soma cumulativa parcial das frequências excede 6,7 para uma procura de 6 unidades.
Tabela 1. Determinação da capacidade óptima de armazém
| Procura ordenada | Frequência | Soma parcial |
|---|---|---|
| 10 | 1 | 1 < 6,7 |
| 9 | 1 | 2 < 6,7 |
| 8 | 2 | 4 < 6,7 |
| 7 | 1 | 5 < 6,7 |
| 6 | 2 | 7 > 6,7 |
| 5 | 1 | 8 > 6,7 |
| 4 | 2 | 10 > 6,7 |
A capacidade óptima do armazém é, portanto, de 6 unidades. O custo total resultante é:
20 × 6 + 2 × 4 + 5 + 2 × 6 + (6 + 4) + 2 × (6 + 2 × 4) + (6 + 3 × 4) + (6 + 4 × 4) = 223 UM.
Se a capacidade for de 5 unidades o custo total é de 224 UM e se a capacidade for de 7 unidades o custo total é de 228 UM.
Suponha-se agora um horizonte de planeamento T = 50, com C0 = 100 UM, C1 = 4 UM e C2 = 8 UM. As necessidades de espaço são dadas na Tabela 2.
20 × 6 + 2 × 4 + 5 + 2 × 6 + (6 + 4) + 2 × (6 + 2 × 4) + (6 + 3 × 4) + (6 + 4 × 4) = 223 UM.
Se a capacidade for de 5 unidades o custo total é de 224 UM e se a capacidade for de 7 unidades o custo total é de 228 UM.
Suponha-se agora um horizonte de planeamento T = 50, com C0 = 100 UM, C1 = 4 UM e C2 = 8 UM. As necessidades de espaço são dadas na Tabela 2.
Tabela 2. Necessidades de espaço de armazenagem
| Períodos | Espaço necessário | Períodos | Espaço necessário |
|---|---|---|---|
| - paletes - | - paletes - | ||
| 1-5 | 100 | 26-30 | 120 |
| 6-10 | 120 | 31-35 | 115 |
| 11-15 | 125 | 36-40 | 110 |
| 16-20 | 130 | 41-45 | 105 |
| 21-25 | 125 | 46-50 | 100 |
Neste caso C' = 100 / (8 - 4) = 25. Na Tabela 3, a soma parcial é igual a 25 quando a procura é igual a 120. Dado que a soma parcial é igual a C', há múltiplas soluções óptimas, nomeadamente, 115 ≤ Q ≤ 120.
Tabela 3. Determinação da capacidade optima de armazém
| Procura ordenada | Frequência | Soma parcial |
|---|---|---|
| 130 | 5 | 5 < 25 |
| 125 | 10 | 15 < 25 |
| 120 | 10 | 25 = 25 |
| 115 | 5 | 30 > 25 |
| 110 | 5 | 35 > 25 |
FRANCIS, Richard L. et al. - Facility Layout and Location: An Analytical Approach, 2.ª ed., Englewood Cliffs, NJ, Prentice Hall, 1992.
SLP de unidade produtiva (II)
A carta de inter-relações para a unidade produtiva é apresentada na Figura 1.
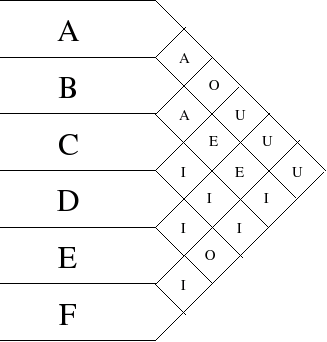
Com a carta de inter-relações, constrói-se o diagrama de inter-relações. Primeiro, constrói-se o diagrama com as relações do tipo A (Figura 2).
Em seguida, constrói-se o diagrama com as relações do tipo A e do tipo E (Figura 3), fazendo os rearranjos necessários.
No terceiro passo, constrói-se o diagrama com as relações do tipo A, E e I (Figura 4), fazendo os rearranjos necessários.
No quarto e último passo, é construído o diagrama de inter-relações (Figura 5), fazendo, novamente, os rearranjos necessários.
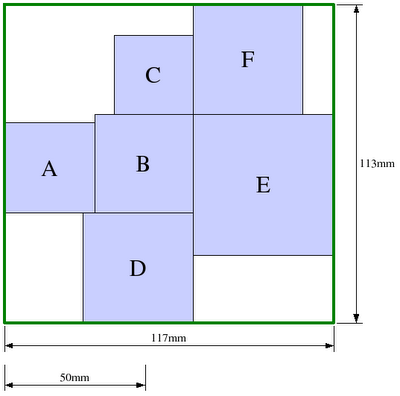
Com o diagrama de inter-relações com uma disposição dos departamentos satisfatória, desenha-se o diagrama de inter-relações de espaços, tendo em conta os espaços necessários e o espaço disponível que, neste caso, são iguais. O resultado é apresentado na Figura 6.
Não havendo nenhumas considerações de mudança nos dados, a limitação prática é que para construir uma instalação com os departamentos nesta disposição, é necessário um espaço de 117 × 113 = 13 221 ft2, enquanto a soma das áreas de todos os departamentos é 8 000 ft2. Há um grande desperdício de espaço e um perímetro irregular, sinónimo de custos mais elevados de manutenção. Condicionando a razão entre as dimensões do departamento C a não ser superior a 2, procede-se da seguinte forma:
L × A = 800 ft2
com
L = largura
A = altura
Então, de
2 A × A = 800
obtém-se:
A = 20 ft e L = 800 / 20 = 40 ft
As dimensões dos outros departamentos são determinadas pela seguinte ordem:
- C
- B
- A
- D
- F
- E
f = altura do departamento F
e = altura do departamento E
l = largura comum ao dois departamentos
Resolvendo o sistema de equações:
Um layout alternativo é apresentado na Figura 7.
Este layout não deve ser tomado como único, mas sim como uma de várias alternativas de layouts para serem avaliados, posteriormente.
SLP de unidade produtiva (I)
A empresa Muitos Produtos Lda. fabrica vários produtos. No processamento requerido pelos produtos estão envolvidos seis departamentos. Na Tabela 1 é apresentado um resumo das sequências de processamento necessárias para os 10 principais produtos e os volumes das produções mensais.
Tabela 1. Sequências e volumes de produção
| Produto | Sequência de processamento | Produção mensal |
|---|---|---|
| 1 | A B C D E F | 800 |
| 2 | A B C B E D C F | 1 000 |
| 3 | A B E F | 600 |
| 4 | A B C E B C F | 2 000 |
| 5 | A C E F | 1 500 |
| 6 | A B C D E F | 400 |
| 7 | A B D E C B F | 2 000 |
| 8 | A B C B D B E B F | 2 500 |
| 9 | A B C D F | 800 |
| 10 | A B D E F | 1 000 |
Na Tabela 2 são apresentadas as áreas necessárias para cada departamento.
Tabela 2. Áreas dos departamentos
| Departamento | Área (ft2) |
|---|---|
| A | 1 000 |
| B | 1 200 |
| C | 800 |
| D | 1 500 |
| E | 2 500 |
| F | 1 500 |
Com base nos dados da Tabela 1 constrói-se a carta de - para (Tabela 3), somando os valores dos volumes movimentados de uma secção para outra:
| Departamentos | Movimentações |
|---|---|
| A para B | 800 + 1 000 + 600 + 2 000 + 400 + 2 000 + 2 500 + 800 + 1 000 = 11 100 |
| B para C | 800 + 1 000 + 2 000 + 2 000 + 400 + 2 500 + 800 = 9 500 |
| B para D | 2 000 + 2 500 + 1 000 = 5 500 |
| B para E | 1 000 + 600 + 2 500 = 4 100 |
| B para F | 2 000 + 2 500 = 4 500 |
| C para B | 1 000 + 2 000 + 2 500 = 5 500 |
| C para D | 800 + 400 + 800 = 2 000 |
| C para E | 2 000 + 1 500 = 3 500 |
| C para F | 1 000 + 2 000 = 3 000 |
| D para E | 800 + 400 + 2 000 + 1 000 = 4 200 |
| E para B | 2 000 + 2 500 = 4 500 |
| E para F | 800 + 600 + 1 500 + 400 = 3 300 |
Tabela 3. Carta de - para
| de - para | A | B | C | D | E | F |
|---|---|---|---|---|---|---|
| A | 11 100 | 1 500 | ||||
| B | 9 500 | 5 500 | 4 100 | 4 500 | ||
| C | 5 500 | 2 000 | 3 500 | 3 000 | ||
| D | 2 500 | 1 000 | 4 200 | 800 | ||
| E | 4 500 | 2 000 | 1 000 | 3 300 | ||
| F |
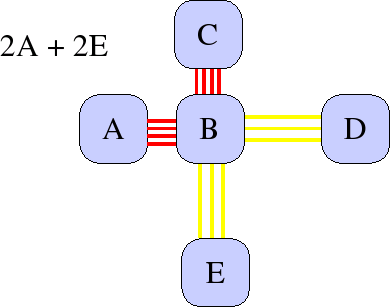
A partir da carta de - para, resume-se a informação numa carta de movimentações entre os departamentos, apresentada na Figura 1.
Com a tabela de movimentações construída, classifica-se a intensidade do fluxo entre os departamentos em cinco classes; A, E, I, O, U por ordem decrescente de importância (Figura 2):
Com o fluxo classificado por intensidade, pode-se, então, construir a carta de inter-relações.
Selecção do tipo de layout por análise do ponto de equilíbrio
A Task Masters Lda. fabrica produtos para segurança. A gestão está a considerar a opção de construir um novo edifício para satisfazer o que parce ser um aumento sustentado da procura de algemas em algumas cidades grandes. A gestão tem que optar entre comprar as algemas a outra empresa e usar o novo edifício para testes de controlo de qualidade, pintura do logotipo da empresa, embalagem e similares; ou usar o novo edifício para produção com um layout do tipo produto ou processo.
Para ajudar na decisão, foi recolhida a seguinte informação
| Alternativas | Custos fixos | Custo unitário* |
|---|---|---|
| - UM / ano - | - UM - | |
| Comprar | 50 000 | 10 |
| Produção com layout tipo processo | 75 000 | 7 |
| Produção com layout tipo produto | 110 000 | 4 |
| * Linear até às 50 000 unidades por ano, o valor máximo previsto para a procura | ||
Para resolver este problema, começa-se por determinar as equações que exprimem o custo total (yi) de cada alternativa (i), em função da quantidade produzida (x):
y1 = 50 000 + 10 x
y2 = 75 000 + 7 x
y3 = 110 000 + 4 x
Onde 1 é a alternativa de comprar; 2, produzir com um layout tipo processo; e 3, produzir com um layout tipo produto.
As três equações acima podem ser representadas graficamente, como se mostra na Figura 1. dado que os menores custos se encontram nos segmentos de recta mais baixos, os pontos de equilíbrio são na intersecção das equações de y1 com y2 e y2 com y3.
 Figura 1. Relação entre o custo e a quantidade produzida anualmente para os layouts alternativos
Figura 1. Relação entre o custo e a quantidade produzida anualmente para os layouts alternativos(carregar com o cursor na figura para ver em tamanho grande)
O valor de x na intersecção entre y1 e y2 pode ser obtido resolvendo a equação
50 000 + 10 x = 75 000 + 7 x
de onde x = 8 33(3) unidades / ano
O valor de x na intersecção entre y2 e y3 é dado por
75 000 + 7 x = 110 000 + 4 x
portanto, x = 11 66(6) unidades / ano.
Pode, então, concluir-se que para:
x ≤ 8 33(3) unidades / ano, a alternativa de menor custo é comprar a outra empresa; para
8 33(3) ≤ x ≤ 11 66(6) unidades / ano, produção com um layout tipo processo; e para
x ≥ 11 66(6) unidades / ano, produção com um layout tipo produto.
OLSEN, Robert A. - Manufacturing Management: A Quantitative Approach, Scranton, PA, International Textbook, 1968, p. 314.
Planeamento do layout de armazém
As distâncias podem ser minimizadas guardando os artigos em áreas de armazenagem em profundidade e posicionando os materiais de forma a minimizar a distância total percorrida. Conforme é ilustrado na Figura 1, armazenando os artigos em áreas de armazenagem em profundidade, a distância percorrida será menor do que se os materiais forem armazenados em áreas sem profundidade.
 Figura 1. Impacte da armazenagem em profundidade na distância percorrida
Figura 1. Impacte da armazenagem em profundidade na distância percorrida(carregar com o cursor na figura para ver em tamanho grande)
A centralização das operações de recepção e expedição, também tem influência nos custos de operação do armazém, como se pode observar na Figura 2.

Figura 2. Impacte da centralização da recepção/expedição
conjugada com a armazenagem dedicada por classes
(carregar com o cursor na figura para ver em tamanho grande)
TOMPKINS, James A.; WHITE, John A. - Facilities Planning, Nova Iorque, John Wiley & Sons, 1984.
Layout óptimo com armazenagem dedicada
Considere-se um armazém cuja planta é ilustrada na Figura 1.
Os locais para armazenagem têm dimensões de 20 × 20 pés. As portas P1 e P2 são para camiões e as portas P3 e P4 são para vagões de caminho de ferro. É usada armazenagem dedicada. Sessenta por cento de todas as movimentações do armazém são feitas pelas portas P1 e P2, tendo cada porta a mesma probabilidade de ser usada. Quarenta por cento de todas as movimentações do armazém são divididas igualmente pelas portas P3 e P4.
Neste armazém vão ser armazenados três produtos, A, B e C, com um único tipo de produto armazenado no mesmo local. O produto A necessita de 3 600 pés2 de espaço de armazenagem e é movimentado à taxa de 750 unidades de carga por mês; o produto B necessita de 6 400 pés2 de espaço de armazenagem e é movimentado à taxa de 900 unidades de carga por mês; o produto C necessita de 4 000 pés2 e é movimentado à taxa de 800 unidades de carga por mês.
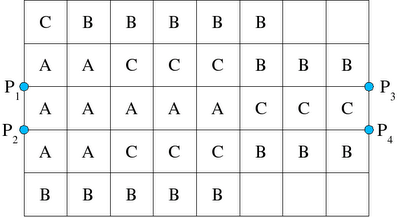
A distância apropriada é a rectilinear, medida entre as portas e os centróides dos locais de armazenagem. Os valores de fk (distância média do local de armazenagem k às portas) estão apresentados na Figura 2. Para exemplificar o cálculo de um fk, suponha-se que k = 29. Medindo as distâncias rectilineares do centróide do local de armazenagem 29 a cada uma das quatro portas tem-se d1, 29 = 120, d2, 29 = 100, d3, 29 = 100 e d4, 29 = 80. Então,
Neste armazém vão ser armazenados três produtos, A, B e C, com um único tipo de produto armazenado no mesmo local. O produto A necessita de 3 600 pés2 de espaço de armazenagem e é movimentado à taxa de 750 unidades de carga por mês; o produto B necessita de 6 400 pés2 de espaço de armazenagem e é movimentado à taxa de 900 unidades de carga por mês; o produto C necessita de 4 000 pés2 e é movimentado à taxa de 800 unidades de carga por mês.
A distância apropriada é a rectilinear, medida entre as portas e os centróides dos locais de armazenagem. Os valores de fk (distância média do local de armazenagem k às portas) estão apresentados na Figura 2. Para exemplificar o cálculo de um fk, suponha-se que k = 29. Medindo as distâncias rectilineares do centróide do local de armazenagem 29 a cada uma das quatro portas tem-se d1, 29 = 120, d2, 29 = 100, d3, 29 = 100 e d4, 29 = 80. Então,
f29 = 0,3 (120) + 0,3 (100) + 0,2 (100) + 0,2 (80) = 102
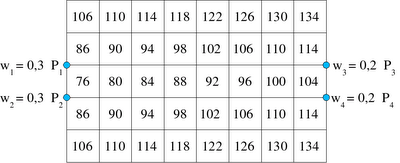
Figura 2. Distância média de cada local de armazenagem k às portas

Figura 2. Distância média de cada local de armazenagem k às portas
O número de locais de armazenagem necessário para cada produto é SA = 3 600 / 400 = 9, SB = 16 e SC = 10. Os valores de Tj são TA = 750, TB = 900, TC = 800. Portanto, os valores de Tj / Sj são TA / SA = 83 1/3, TB / SB = 56,25 e TC / SC = 80. Então os produtos são numerados 1(A), 2(C) e 3(B).
O produto 1(A) necessita de 9 locais de armazenagem; então, os locais de armazenagem afectados ao produto A são [17, 18, 19, 9, 25, 20, 10, 26, 21]. O produto 2(C) necessita de 10 locais de armazenagem; então, [11, 27, 22, 12, 28, 23, 13, 29, 24, 1] são afectados ao produto C. O produto 3(B) necessita de 16 locais de armazenagem; então, o produto B é afectado aos locais de armazenagem [14, 30, 33, 2, 15, 31, 34, 3, 16, 32, 35, 4, 36, 5, 37, 6]. Os locais 7, 8, 38, 39 e 40 ficam disponíveis para armazenar equipamento, sanitários, escritórios e outros.
Um layout que minimiza a distância média percorrida por unidade de tempo é mostrado na Figura 3. É importante salientar que o layout apresentado não é o único que minimiza a distância média percorrida por unidade de tempo, nem necessariamente o layout final. Nada mais foi considerado, para além da distância média percorrida; a utilização desta abordagem da armazenagem dedicada deve ser examinada em cada aplicação em particular. No entanto, o layout serve de base para a avaliação de outras configurações.
O produto 1(A) necessita de 9 locais de armazenagem; então, os locais de armazenagem afectados ao produto A são [17, 18, 19, 9, 25, 20, 10, 26, 21]. O produto 2(C) necessita de 10 locais de armazenagem; então, [11, 27, 22, 12, 28, 23, 13, 29, 24, 1] são afectados ao produto C. O produto 3(B) necessita de 16 locais de armazenagem; então, o produto B é afectado aos locais de armazenagem [14, 30, 33, 2, 15, 31, 34, 3, 16, 32, 35, 4, 36, 5, 37, 6]. Os locais 7, 8, 38, 39 e 40 ficam disponíveis para armazenar equipamento, sanitários, escritórios e outros.
Um layout que minimiza a distância média percorrida por unidade de tempo é mostrado na Figura 3. É importante salientar que o layout apresentado não é o único que minimiza a distância média percorrida por unidade de tempo, nem necessariamente o layout final. Nada mais foi considerado, para além da distância média percorrida; a utilização desta abordagem da armazenagem dedicada deve ser examinada em cada aplicação em particular. No entanto, o layout serve de base para a avaliação de outras configurações.
TOMPKINS, James A.; WHITE, John A. - Facilities Planning, Nova Iorque, John Wiley & Sons, 1984.
Afectação de produtos a locais de armazenagem dedicada
A configuração óptima dos produtos em armazenagem dedicada envolve a afectação dos produtos aos locais de armazenagem. As distâncias rectilineares são consideradas apropriadas e é usada a seguinte notação:
| q | = | número de locais de armazenagem |
| n | = | número de produtos |
| m | = | número de locais de entrada/saída (cais e/ou portas) |
| Sj | = | número de locais de armazenagem necessários para o produto j |
| Tj | = | número de entradas e saídas do armazém do produto j, isto é, as movimentações do produto j |
| pi | = | percentagem das entradas/saídas do armazém pelo ponto de entrada/saída i |
| dik | = | distância (ou tempo) que é necessário percorrer do ponto i ao local de armazenagem k |
| xjk | = | 1 se o produto j é afectado ao local de armazenagem k; caso contrário, 0 |
| f(x) | = | distância (ou tempo) média percorrida |
O problema do layout do armazém pode ser formulado da seguinte forma:
Minimizar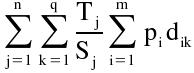
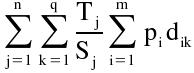
sujeito a:
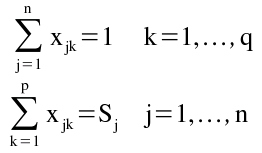
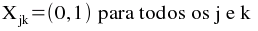
Supõe-se que cada artigo tem igual probabilidade de se movimentar entre o ponto de entrada/saída ou porta i e qualquer local de armazenagem afectado ao artigo j. Portanto, o valor de (1 / Sj) é a probabilidade de um local de armazenagem em particular afectado ao produto j ser escolhido para a movimentação de saída/entrada por uma porta. Fazendo
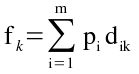
onde fk é a distância média percorrida entre o local de armazenagem k e as portas.
Para minimizar a distância média total percorrida, procede-se do seguinte modo:
Para minimizar a distância média total percorrida, procede-se do seguinte modo:
- Numerar os produtos de acordo com o valor de Tj / Sj, de forma que
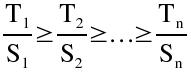
- Calcular os valores de fk para todos os locais de armazenagem.
- Afectar o produto 1 aos S1 locais de armazenagem que têm os menores valores de fk; afectar o produto 2 aos S2 locais de armazenagem que têm os menores valores de fk seguintes e assim sucessivamente.
TOMPKINS, James A.; WHITE, John A. - Facilities Planning, Nova Iorque, John Wiley & Sons, 1984.
Armazenagem aleatória vs dedicada
Para ilustar o efeito do método de armazenagem nas necessidades de espaço, suponha-se que seis produtos são recebidos num armazém. As existências de cada um dos produtos no final de cada período são as apresentadas na Tabela 1. O valor agregado das existências obtém-se somando as existências dos seis produtos.
Tabela 1 - Existências de seis produtos em armazém, expressos em paletes de produto
| Produtos | |||||||
| Período | 1 | 2 | 3 | 4 | 5 | 6 | Agregado |
| 1 | 24 | 12 | 2 | 14 | 11 | 12 | 73 |
| 2 | 22 | 9 | 8 | 8 | 10 | 9 | 66 |
| 3 | 20 | 6 | 6 | 4 | 9 | 6 | 51 |
| 4 | 18 | 3 | 4 | 24 | 8 | 3 | 60 |
| 5 | 16 | 36 | 2 | 20 | 7 | 24 | 105 |
| 6 | 14 | 33 | 8 | 16 | 6 | 21 | 98 |
| 7 | 12 | 30 | 6 | 12 | 5 | 18 | 83 |
| 8 | 10 | 27 | 4 | 8 | 4 | 15 | 68 |
| 9 | 8 | 24 | 2 | 4 | 3 | 12 | 53 |
| 10 | 6 | 21 | 8 | 24 | 2 | 9 | 70 |
| 11 | 4 | 18 | 6 | 20 | 1 | 6 | 55 |
| 12 | 2 | 15 | 4 | 16 | 24 | 3 | 64 |
| 13 | 24 | 12 | 2 | 12 | 23 | 24 | 97 |
| 14 | 22 | 9 | 8 | 8 | 22 | 21 | 90 |
| 15 | 20 | 6 | 6 | 4 | 21 | 13 | 70 |
| 16 | 13 | 3 | 4 | 24 | 20 | 15 | 79 |
| 17 | 16 | 36 | 2 | 20 | 19 | 12 | 105 |
| 18 | 14 | 33 | 8 | 16 | 13 | 9 | 93 |
| 19 | 12 | 30 | 6 | 12 | 17 | 6 | 83 |
| 20 | 10 | 27 | 4 | 8 | 16 | 3 | 68 |
| 21 | 8 | 24 | 2 | 4 | 15 | 24 | 77 |
| 22 | 6 | 21 | 8 | 24 | 14 | 21 | 94 |
| 23 | 4 | 18 | 6 | 20 | 13 | 18 | 79 |
| 24 | 2 | 15 | 4 | 16 | 12 | 15 | 64 |
| Soma dos níveis máximos de existências individuais Nível máximo do valor agregado das existências Nível médio do valor agregado das existências Nível mínimo do valor agregado das existências | = 140 = 105 = 77,5 = 51 | ||||||
Os níveis máximos das existências de cada um dos seis produtos são:
- Produto 1: 24
- Produto 2: 36
- Produto 3: 8
- Produto 4: 24
- Produto 5: 24
- Produto 6: 24
Com armazenagem dedicada o espaço necessário é igual à soma dos valoes máximos das existências de todos os produtos, ou seja espaço para 140 paletes. Com armazenagem aleatória o espaço necessário é igual ao máximo do valor agregado das existências. isto é, espaço para 105 paletes. Neste exemplo, a armazenagem dedicada necessita de mais um terço do espaço necessário com armazenagem aleatória.
TOMPKINS, James A.; WHITE, John A. - Facilities Planning, Nova Iorque, John Wiley & Sons, 1984.
TOMPKINS, James A.; WHITE, John A. - Facilities Planning, Nova Iorque, John Wiley & Sons, 1984.
sexta-feira, junho 09, 2006
Filas de espera (M/M/1): sensibilidade a μ
Um armazém de um hipermercado recebe camiões com encomendas que são descarregados usando empilhadoras. Um levantamento de dados realizado no local permitiu concluir que os camiões chegam seguindo uma distribuição de Poisson, a uma taxa de 16 camiões / dia; os tempos de descarga seguem uma distribuição Exponencial Negativa, com médias que dependem do número de empilhadoras utilizadas:
| N.º de empilhadoras | Tempo de descarga |
| (1 / µ) | |
| --- minutos --- | |
| 1 | 50 |
| 2 | 20 |
| 3 | 15 |
| 4 | 12 |
| 5 | 10 |
A operação das empilhadoras tem um custo de 15 UM / hora e a imobilização dos camiões acarreta um encargo de 30 UM / hora.
1) Trata-se, portanto, de um sistema M/M/1, com λ = 2 camiões / hora.
A taxa de serviço ou taxa de descarga (µ) vai depender da decisão tomada sobre o número de empilhadoras.
2) Verificação da condição de equilíbrio: λ / µ < 1 ⇒ µ > 2 ⇒ Número de empilhadoras ≥ 2
Com uma empilhadora, a taxa de descarga é inferior à taxa de chegada, o que leva ao crescimento ilimitado da fila, nunca se atingindo o estado de equilíbrio.
Com duas ou mais empilhadoras, a condição de equilíbrio (ρ < 1) é satisfeita, permitindo determinar todas as medidas de desempenho para o modelo M / M / 1.
Operando com várias empilhadoras, a fila permanece sempre única, com apenas 1 servidor, devido ao facto das várias empilhadoras descarregam simultaneamente o mesmo camião, traduzindo-se num aumento da velocidade de descarga (aumento de velocidade do servidor ou taxa de serviço, µ).
Na tabela seguinte são indicados, para cada número de empilhadoras, o tempo médio de descarga dado (1 / µ), a taxa de serviço (µ), a taxa de ocupação (ρ = λ / μ), o tempo que, em média, os camiões permanecem no sistema (W) e o número médio de camiões no sistema (L = λ × W)
| N.º de empilhadoras | Tempo médio de descarga | Taxa de serviço | Taxa de ocupação | Tempo médio no sistema por camião | Número médio de camiões no sistema |
| (n) | (1 / µ) | (µ) | (λ / µ) | (W) | (L = λ × W) |
| - minutos - | - camiões por hora - | - horas - | - camiões - | ||
| 1 | 50 | 1,20 | 1,67 | ||
| 2 | 20 | 3,00 | 0,67 | 1,00 | 2,00 |
| 3 | 15 | 4,00 | 0,50 | 0,50 | 1,00 |
| 4 | 12 | 5,00 | 0,40 | 0,33 | 0,67 |
| 5 | 10 | 6,00 | 0,33 | 0,25 | 0,50 |
Para minimizar os custos do sistema, há que determinar o custo de imobilização dos camiões e o custo do serviço, directamente proporcional ao número de empilhadoras utilizadas na descarga.
Na tabela seguinte apresenta-se o custo total em função do número de empilhadoras, permitindo concluir que o custo mínimo, de 75 UM / hora, corresponde a três empilhadoras.
| N.º de empilhadoras | Custo de imobilização dos camiões | Custo das empilhadoras | Custo total |
| (n) | (30 λ w) | (15 n) | |
| -------------- UM / hora ------------- | |||
| 1 | - | - | - |
| 2 | 60 | 30 | 90 |
| 3 | 30 | 45 | 75 |
| 4 | 20 | 60 | 80 |
| 5 | 15 | 75 | 90 |
Filas de espera (M/M/S): funcionamento de cais de armazém
Caso de aplicação
Ao cais de um hipermercado com três docas, chegam camiões com uma distribuição de Poisson a uma taxa de 20 veículos por dia de oito horas. O tempo de carga ou descarga do camião segue uma distribuição exponencial com média de 40 minutos.
1) Trata-se, portanto, de um sistema M/M/3, com taxa de chegadas, λ = 20 veiculos / dia = 2,5 veiculos / hora e taxa de serviço (µ)= 60 / 40 = 1,5 veiculos / hora.
2) Verificação da condição de equilíbrio: ρ = λ / S µ = 2,5 / (3 × 1,5) = 5 / 9 < 1.
As três docas têm, portanto, capacidade para os camiões que se dirigem ao armazém do hipermercado.
Medidas de desempenho
1) Intensidade do tráfego (λ / µ) =
= λ / µ = 2,5 / 1,5 = 5 /3
2) Taxa de ocupação (ρ)=
Taxa média de ocupação do sistema =
Taxa média de ocupação do servidor =
Factor de ocupação do sistema =
ρ = λ / S µ = 2,5 / (3 × 1,5) = 5 / 9
3) Taxa de desocupação (1 - ρ) =
= 1 - ρ = 4 / 9
4) Número médio de camiões no sistema (L) =
L = 2 camiões
5) Número médio de camiões à espera (Lq) =
Lq = 0,4 camiões
6) Tempo médio no sistema (W) =
W = 0,8 horas = 49 minutos
7) Tempo médio à espera (Wq) =
Wq = 0,15 horas = 9 minutos
8) Número médio de camiões a serem servidos (L3) =
Número médio de cais ocupados (Lb) =
L3 = 5 / 3 camiões
Lb = 5 / 3 cais
9) Probabilidade de não existir nenhum camião no sistema (P0) =
P0 = 17 %
10) Probabilidade de existir algum camião no sistema (P {n > 0}) =
= 1 - P0 = 83 %
11) Probabilidade de ter que esperar (Pw) =
Probabilidade do sistema estar ocupado (Pb) =
Probabilidade de todos os servidores estarem ocupados =
Pw = Pb = 30 %
12) Probabilidade de não ter que esperar (1 - Pw) =
Probabilidade de um servidor estar desocupado (1 - Pb) =
1 - Pw = 1 - Pb = 70 %
13) Probabilidade de n servidores (0 ≤ n ≤ 3) estarem ocupados =
Probabilidade de haver n camiões (0 ≤ n ≤ 3) no sistema =
| n | 0 | 1 | 2 | 3 |
| Pn | 0,1727 | 0,2878 | 0,2398 | 0,1332 |
14) Probabilidade de n servidores (0 ≤ n ≤ 3) estarem desocupados =
Probabilidade de haver (3 - n) camiões (0 ≤ n ≤ 3) no sistema =
| n | 3 | 2 | 1 | 0 |
| 3 - n | 0 | 1 | 2 | 3 |
| Pn | 0,1727 | 0,2878 | 0,2398 | 0,1332 |
15) Número médio de camiões à espera, quando o sistema está ocupado (Lb) =
Lb = 1,25 camiões
16) Número médio de camiões à espera, quando há pelo menos um (Lq | q > 0) =
Lq | q > 0 = 2,25 camiões
17) Tempo médio à espera, quando o sistema está ocupado (Wb) =
Tempo médio à espera, quando se tem de esperar =
Wb = 0,5 horas
18) Probabilidade de haver 0, 1, 2, …, n camiões no sistema (Pn)
19) Probabilidade de não haver mais de n (n ou menos) camiões no sistema (P {N ≤ n})
20) Probabilidade de haver mais de n camiões no sistema ((P {N > n}) =
1 - Probabilidade de não haver mais de n (n ou menos) camiões no sistema =
1 - (P {N ≤ n})
Probabilidade de haver pelo menos n + 1 (n + 1 ou mais) camiões no sistema (P {N ≥ n + 1})
21) Probabilidade de haver pelo menos n (n ou mais) camiões no sistema (P {N ≥ n})
| n | Pn | P {N ≤ n} | P {N ≥ n} | q | Pq | P {Q ≤ q} | P {Q ≥ q} |
| (18) | (19) | (21) | (23) | (24) | (25) | ||
| 0 | 0,17 | 0,17 | 1,00 | ||||
| 1 | 0,29 | 0,46 | 0,83 | ||||
| 2 | 0,24 | 0,70 | 0,54 | ||||
| 3 | 0,13 | 0,83 | 0,30 | 0 | 0,13 | 0,83 | 0,30 |
| 4 | 0,07 | 0,91 | 0,17 | 1 | 0,07 | 0,91 | 0,17 |
| 5 | 0,04 | 0,95 | 0,09 | 2 | 0,04 | 0,95 | 0,09 |
| 6 | 0,02 | 0,97 | 0,05 | 3 | 0,02 | 0,97 | 0,05 |
| 7 | 0,01 | 0,98 | 0,03 | 4 | 0,01 | 0,98 | 0,03 |
| 8 | 0,01 | 0,99 | 0,02 | 5 | 0,01 | 0,99 | 0,02 |
| 9 | 0,00 | 1,00 | 0,01 | 6 | 0,00 | 1,00 | 0,01 |
| 10 | 0,00 | 1,00 | 0,00 | 7 | 0,00 | 1,00 | 0,00 |
22) Probabilidade de haver n camiões a serem servidos =
Pn, para 0 ≤ n < S
PS = 1 - ∑(S - 1)Pn, para n = S
| n | 0 | 1 | 2 | 3 |
| Pn | 0,17 | 0,29 | 0,24 | 0,30 |
23) Probabilidade de haver 3 camiões a serem servidos e q na fila =
Probabilidade de haver 0, 1, 2, 3,…, q camiões na fila (P {Q = q}) =
P3, para q = 0
Pq + 1, para q = 1, 2, 3,…
24) Probabilidade de não haver mais de q (q ou menos) camiões na fila (P {Q ≤ q})
25)Probabilidade de haver pelo menos q (q ou mais) camiões na fila (P {Q ≤ q})
Na figura seguinte podem ver-se algumas das medidas de desempenho do problema acima, determinadas numa folha de cálculo pré-programada (McClain, 2003).

Filas de espera: M/M/S vs S sistemas M/M/1
No caso do talho/charcutaria do hipermercado, considere-se as seguintes alternativas:
A. Uma senha (fila única) e duas empregadas, ou seja, um sistema com dois servidores.
B. Duas senhas (duas filas) e uma empregada para cada senha, isto é, dois sistemas de um servidor. Neste caso supôe-se que os clientes se dividem igualmente pelos dois sistemas, portanto λB = λA / 2.
| Medidas de | M/M/2 | 2 × M/M/1 |
| desempenho | λA = 0,5 cl. / min. | λB = 0,25 cl. / min. |
| L (clientes) | 0,87 | 1,2 (= 2 × 0,6) |
| Lq (clientes) | 0,12 | 0,45 (= 2 × 0,225) |
| W (minutos) | 1,75 | 2,4 |
| Wq (minutos) | 0,25 | 0,9 |
Com um sistema de dois servidores (alternativa A) verifica-se uma redução substancial nas quatro medidas de desempenho, em relação a dois sistemas, cada um com a sua fila.
Sempre que possível, é preferível ter um sistema com múltiplos servidores e uma fila única, do que ter o mesmo número de servidores, cada um a atender uma fila.
As duas alternativas têm os mesmos custos (não contando o custo e manutenção de uma máquina de senhas), mas grandes diferenças na previsível satisfação dos clientes. Os clientes, em geral, dão mais importância, pela negativa, ao tempo que permanecem na fila à espera.
Filas de espera (M/G/1): variabilidade do serviço
A variabilidade do serviço tem um efeito importante nas medidas de desempenho do sistema, para além da velocidade média do servidor. Compare-se o desempenho de três sistemas com variâncias do tempo de serviço crescentes.
| Medidas de | σ2 = 0 | σ2 = 2,25 | σ2 = (2,25)2 |
| desempenho | (M/D/1) | (M/M/1) | |
| ρ | 0,75 | 0,75 | 0,75 |
| P0 | 0,25 | 0,25 | 0,25 |
| L (clientes) | 1,875 | 3 | 4,4 |
| Lq (clientes) | 1,125 | 2,25 | 3,66 |
| W (minutos) | 3,75 | 6 | 8,8 |
| Wq (minutos) | 2,25 | 4,5 | 7,3 |
| Lb (clientes) | 1,5 | 3 | 4,875 |
| Wb (minutos) | 3 | 6 | 9,75 |
O número médio de clientes no sistema (L), na fila (Lq), na fila, quando o sistema está ocupado (Lb), o tempo no sistema (W), na fila (Wq) e na fila, quando o sistema está ocupado (Wb), aumentam (linearmente) com a variância, e só dependem da taxa de chegadas, intensidade de tráfego e variância do serviço.
A variabilidade do servidor tem um efeito importante nas medidas de desempenho do sistema, para além da velocidade média do servidor.
Considerando a variância nula (M/D/1), o tamanho médio da fila (Lq), número médio de clientes na fila, quando o sistema está ocupado (Lb), o tempo médio na fila (Wq) e na fila, quando o sistema está ocupado (Wb), são exactamente metade dos valores para M/M/1.
Diminuir a variância pode, portanto, melhorar significativamente as medidas de desempenho do sistema.
quarta-feira, junho 07, 2006
Filas de espera (M/G/1): medidas de desempenho
Num hipermercado, a certas horas do dia, os clientes dirigem-se a uma caixa registadora, para pagar as compras, com uma distribuição de Poisson, a uma taxa média de um de dois em dois minutos. A empregada da caixa atende os clientes por ordem de chegada (FIFO). Dado o tempo gasto a fazer as compras, os clientes estão dispostos a esperar para serem atendidos, se for necessário. O tempo de atendimento de cada cliente é, em média, 1,5 minutos, com uma variância de (9 / 4)2.
1) Trata-se, portanto, de um sistema M/G/1, com taxa de chegadas λ = 0,5 clientes / minuto e tempo médio de serviço (1 / μ) = 1,5 minutos, com uma variância σ2= (9 / 4)2.
2) Verificação da condição de equilíbrio: ρ = λ / μ = 0,5 × 1,5 = 0,75 < 1.
A empregada tem, portanto, capacidade para atender os clientes que se dirigem à caixa para pagar as compras. O sistema poderá atingir o estado estacionário, se as condições dadas se mantiverem por tempo suficiente. A fila de espera não cresce indefinidamente, mas varia de tamanho ao longo do tempo.
Medidas de desempenho
1) Taxa de ocupação (ρ) =
Taxa média de ocupação do sistema =
Taxa média de ocupação do servidor =
Factor de ocupação do sistema =
Intensidade do tráfego =
Probabilidade de existir algum cliente no sistema (P {n > 0}) =
Probabilidade de ter que esperar na fila (Pw) =
Probabilidade do servidor estar ocupado (Pb) =
ρ = λ / μ = 0,75
2) Taxa de desocupação (P0) =
Probabilidade de não existir nenhum cliente no sistema =
Probabilidade de não ter que esperar na fila =
Probabilidade do servidor estar desocupado =
P0 =1 - ρ = 0,25
3) Número médio de clientes no sistema (L) =
L = {(λ2 σ2 + ρ2) / [2 (1 - ρ)]} + ρ = 4,4 clientes
4) Número médio de clientes na fila (Lq) =
Tamanho médio da fila =
Lq = (λ2 σ2 + ρ2) / [2 (1 - ρ)] = 3,7 clientes
5) Tempo médio no sistema (W) =
Duração média do período de ocupação do servidor =
W = L / λ = 8,8 minutos
6) Tempo médio na fila (Wq) =
Tempo médio de espera na fila =
Wq = Lq / λ = 7,3 minutos
7) Número médio de clientes na fila, quando o sistema está ocupado (Lb) =
Lb = Lq / Pw = 4,875 clientes
8) Número médio de clientes na fila, quando há pelo menos um (Lq | q > 0) =
Número médio de clientes servidos por período de ocupação do servidor =
Lq | q > 0 = μ W = 5,875 clientes
9) Número médio de clientes a serem servidos (LS) =
Número médio de servidores ocupados (Sb) =
LS = L - Lq = ρ = 0,75 clientes
Sb = ρ = Pb = 0,75 servidores
10) Tempo médio na fila, quando o sistema está ocupado (Wb) =
Tempo médio na fila, quando se tem de esperar =
Wb = Wq / Pw = 7,3125 / 0,75 = 9,75 minutos
11) Probabilidade de haver 0, 1, 2, …, n clientes no sistema (Pn)
12) Probabilidade de não haver mais de n (n ou menos) clientes no sistema (P {N ≤ n})
13) Probabilidade de haver mais de n clientes no sistema (P {N > n}) =
1 - Probabilidade de não haver mais de n (n ou menos) clientes no sistema = 1 - (P {N ≤ n})
Probabilidade de haver pelo menos n + 1 (n + 1 ou mais) clientes no sistema (P {N ≥ n + 1}) =
ρn + 1
14) Probabilidade de haver pelo menos n (n ou mais) clientes no sistema (P {N ≥ n}) =
ρn, para n = 0, 1, 2, …
| Pn | P {N ≤ n} | P {N ≥ n} | Pq | P {Q ≤ q} | P {Q ≥ q} | ||
| n | (11) | (12) | (14) | q | (16) | (17) | (18) |
| 0 | 0,25 | 0,25 | 1,00 | ||||
| 1 | 0,19 | 0,44 | 0,75 | 0 | 0,19 | 0,44 | 0,75 |
| 2 | 0,14 | 0,58 | 0,56 | 1 | 0,14 | 0,58 | 0,56 |
| 3 | 0,11 | 0,68 | 0,42 | 2 | 0,11 | 0,68 | 0,42 |
| 4 | 0,08 | 0,76 | 0,32 | 3 | 0,08 | 0,76 | 0,32 |
| 5 | 0,06 | 0,82 | 0,24 | 4 | 0,06 | 0,82 | 0,24 |
| 6 | 0,04 | 0,87 | 0,18 | 5 | 0,04 | 0,87 | 0,18 |
| 7 | 0,03 | 0,90 | 0,13 | 6 | 0,03 | 0,90 | 0,13 |
| 8 | 0,03 | 0,92 | 0,10 | 7 | 0,03 | 0,92 | 0,10 |
| 9 | 0,02 | 0,94 | 0,08 | 8 | 0,02 | 0,94 | 0,08 |
| 10 | 0,01 | 0,96 | 0,06 | 9 | 0,01 | 0,96 | 0,06 |
| 11 | 0,01 | 0,97 | 0,04 | 10 | 0,01 | 0,97 | 0,04 |
| 12 | 0,01 | 0,98 | 0,03 | 11 | 0,01 | 0,98 | 0,03 |
| 13 | 0,01 | 0,98 | 0,02 | 12 | 0,01 | 0,98 | 0,02 |
| 14 | 0,00 | 0,99 | 0,02 | 13 | 0,00 | 0,99 | 0,02 |
| 15 | 0,00 | 0,99 | 0,01 | 14 | 0,00 | 0,99 | 0,01 |
15) Probabilidade de haver um cliente a ser servido e nenhum na fila =
P1 = 0,19
16) Probabilidade de haver um cliente a ser servido e q na fila =
Probabilidade de haver 0, 1, 2, …, q clientes na fila (P {Q = q}) =
P1, para q = 0
Pq + 1, para q = 1, 2, …
17) Probabilidade de não haver mais de q (q ou menos) clientes na fila (P {Q ≤ q}) =
Confiar que há espaço para q clientes esperarem, uma percentagem (probabilidade × 100) do tempo =
P {N ≤ q + 1}
Se quisermos estar confiantes de que há espaço no hipermercado para os clientes de uma caixa, pelo menos 95% do tempo, devemos ser capazes de acolher 10 clientes, incluindo o que está a ser servido, ou seja, haver espaço para uma fila de 9 clientes com os carros das compras.
18) Probabilidade de haver pelo menos q (q ou mais) clientes na fila (P {Q ≥ q}) =
P {N ≥ q + 1} = ρq + 1
domingo, junho 04, 2006
Equipamentos para hipermercados (V)
Expositores, produzidos pela Avedol - Indústria de estantes e expositores, essencialmente utilizados para dar maior destaque ao produto.
| Modelo | Altura x Profundidade x Largura (mm) |
| Expositor A1 | 600 x 230 x 190 |
| Expositor A2 | 330 x 200 x 140 |
| Expositor A3 | 650 x 160 x 120 |
| Expositor Q | 1 600 x 450 x 580 |
| Expositor tubo01 | 1 660 x 410 x 500 |
| Expositor tubo02 | 1 660 x 450 x 500 |
| Expositor tubo03 | 1 660 x 410 x 500 |
| Expositor tubo04 | 1 660 x 450 x 500 |
| Expositor tubo05 | 1 600 x 450 x 580 |
| Expositor balcão rotativo01 | 400 x 300 x 500 |
| Expositor balcão rotativo03 | 400 x 150 x 300 |
| Expositor checkout 900 | 1 400 x 500 x 900 |
Expositores neutros / quentes de bancada, utilizados nas zonas de pastelaria, padaria e pizzaria, comercializados pela Fridouro.
| Modelo | Altura x Profundidade x Largura (mm) | Tipo |
| ECC | 195 x 370 x 1 020 | Neutro |
| EO | 235 x 210 x 1 000 | Neutro |
| VEM 510 Inox | 200 x 350 x 500 | Neutro |
| VEM 520 Inox | 340 x 350 x 500 | Neutro |
| CT4C | 235 x 385 x 810 | Quente |
| CTEE | 470 x 600 x 1 150 | Quente |
| VEC 520 | 410 x 350 x 500 | Quente |
| RIT | 610 x 470 x 470 | Quente |